An estimation about number of zeros

Mittag-Leffler thm과 Weierstrauss thm은 zero or pole이 임의로 취해질 수 잇다는(물론 limit point 제외) 긍정적 결과를 내놓는다. 그러나 zero의 분포는 해당함수의 growth rate에 영향을 주기 때문에 우리가 growth rate마저 임의로 선택할 수 없다. essence는 Jensen`s formula로부터 온다.

떡밥 하나.

 

혹시 읽는 사람이 잇다면 스스로 증명해보시길...

Jensen`s formula.

f가 open disc D(0:R)에서 holomorphic하고 f(0)가 nonzero, r을 0보다 크고 R보다 작은 어떤 수라 하자. 에 잇는 f의 zero를 중복도를 다 카운팅해서 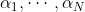라 하자. 그러면 다음이 성립한다.

 

증명은 보조함수 하나 잡아서 거의 한방에 끝낸다.

  까지는 크기가 r보다 작고 는 크기가 r이라 하자.

라 하면, 얘는 에서 holomorphic라고 zero가 없다. 따라서, D는 simply connected이므로 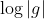는 D에서 harmonic이다. mean value property를 쓰기 전에 저 g를 왜 저리 잡앗는지 생각해보자. 사실, 에서 자기자신으로 가는 대표적인 conformal mapping을 알고잇으면(알파가 1보다 작을때, . 그리고 얘는 boundary를 보존한다.) 그 이유를 어렵지 않게 알수 잇다. 지금 open disc D(0;r)에서 놀고잇으니 1/r배로 줄여주는 함수와 합성하면 저 중간 이상하게 생긴 factor의 역수가 나온다.(왜 역수를 취해줫는고 하니 당연히 zero를 다 remove하려고...)

다시 돌아가서 MVT는

 

임을 말하고, 이제 g대신에 다 f텀으로 대입하면 원하는 식을 얻는다...

zero와 r-circle 상의 f의 크기와의 관계를 얻어냇다.

f가 entire function, n(r)을 크기가 r이하의 zeros of f의 개수, 라 놓고서 가시적인 estimation을 해보자. (편의상 f(0)=1이라 하겟다)

 

(여기서 내가 zero수열을 크기가 nondecreasing하게 잡앗다. 왜 항상 zero set은 countable인가 등등 이런 종류의 질문은 compact set의 성질과 holomorphic function의 성질로부터 오는데 요런건 다 생략...)

위 부등식을 다시 쓰면,

그니까 f가 근을 많이 가지면 f는 좀더 '출렁이는' 놈이다. 가령 f가 충분히 큰 z에 대해로 bound되면 다시 log을 취함으로써 다음을 얻는다

 

(이 구체적인 예시에서는 저 estimation을 optimal하다.

예를 들어, 로 잡으면 저 등호가 딱 성립한다.)

요런 estimation을 보면서 참 해석학자들은 일이 참 힘들거란 느낌을 받는다.

예를 하나 더 들어보자. 이번에는 반대로 근부터 assign해보자.

f가 entire하고,  (n=1,2,3,...), 충분히 큰 z에 대해서, 라 해보자.

저런 nonzero f가 있기 위해서는 저 alpha는 어떤 조건을 만족시켜야 하는가.

을 대입하면 alpha는 2 이상이어야 하고, 는 alpha가 2보다 클 경우에 저 가정을 모두 만족시킨다. alpha가 2인 경우엔 어떨까.